ما هو المثلث
- يعتبر المثلث من الأشكال الهندسية الأساسية، ويعتبر حساب مساحة المثلث من الأشياء التي عُرفت منذ القدم، لأنه من أهم الأشكال الهندسية التي تمكن من وجود العديد من الأشكال الهندسية الفرضيات الرياضية.
- يتكون المثلث من ثلاثة جوانب، وهو عبارة عن شكل هندسي ثنائي الأبعاد، ومجموع زوايا المثلث دائمًا 180 درجة، ويقسم حسب شكل أضلاع المثلث وزواياها المختلفة.
- بالنسبة لأولئك الذين يسألون عن كيفية حساب مساحة المثلث، فهو يتكون من عدد من الوحدات المربعة، ويمكن اعتبار هذه المنطقة من مناطق ذات بعدين، حيث توجد قواعد رياضية أساسية لحساب المنطقة.
- الطريقة الأساسية لحساب مساحة المثلث هي ضرب طول القاعدة في ارتفاع المثلث، ثم تقسيمها على الرقم 2، لكن هذه القاعدة لمثلث متساوي الأضلاع فقط.
- أما بالنسبة لكيفية حساب مساحة المثلث ذي المساحات والأشكال المختلفة، فهذه المسألة لها العديد من القواعد الأساسية، والتي تختلف في أضلاع وزوايا المثلث المختلفة.
أنواع المثلثات
1- أنواع المثلثات حسب الأضلاع
- المثلث المتساوي الأضلاع: هذا النوع تكون فيه جميع جوانب المثلث متساوية في الطول والزوايا، وفي معظم الأحيان تكون زوايا المثلث متساوي الأضلاع 60 درجة.
- المثلث متعدد الأضلاع: وهو النوع الذي تختلف فيه جميع الأضلاع في الطول والزوايا، وتتفاوت درجاتها بشكل كبير فيما بينها لتساوي في النهاية مجموعها 180 درجة.
- مثلث متساوي الساقين: هذا النوع له ساقان متساويتان في الطول بدقة، والضلع الثالث هو الذي يختلف اختلافًا كبيرًا عنهما في الطول، ليكون صلة بين زاويتين محصورتين في المثلث.
2- أنواع المثلثات حسب الزوايا
- مثلث حاد الزاوية: هذا النوع به جميع زوايا المثلث أقل من 90 درجة، وفي هذا النوع من المثلثات تكون درجات الزوايا الثلاث متساوية في الدرجة.
- مثلث قائم الزاوية: في هذا النوع من المثلثات، توجد زاوية واحدة قياسها 90 درجة، والزاويتان الأخريان في المثلث أقل من 90 درجة، أي أنها تشكل زوايا حادة.
- مثلث الوجه: في هذا النوع توجد زاوية واحدة في المثلث أكبر من 90 درجة، والزاويتان المتبقيتان أقل من 90 درجة، أي أنها من زوايا حادة.
كيف تحسب مساحة المثلث
- مع الاختلاف الكبير في أنواع المثلثات المختلفة، سواء من حيث الأضلاع أو الزوايا، فإن لدى الكثير من الناس تساؤل حول كيفية حساب مساحة المثلث، لأن هناك العديد من الطرق والقوانين المختلفة المستخدمة في ذلك.
- نظرًا لأن هذه القواعد والطرق تحسب المساحة التي تشغلها هذه المثلثات للوحدات المربعة المختلفة، ووفقًا للبيانات التي لدينا حول كل مثلث، فإننا نحسب مساحته.
1- باستخدام القاعدة والارتفاع
- تعتبر طريقة استخدام القاعدة والارتفاع من أهم الطرق والقواعد التي يتم استخدامها هندسيًا لمعرفة كيفية حساب مساحة المثلث، والتي يوجد بها قاعدة رياضية أساسية يمكن الاعتماد عليها.
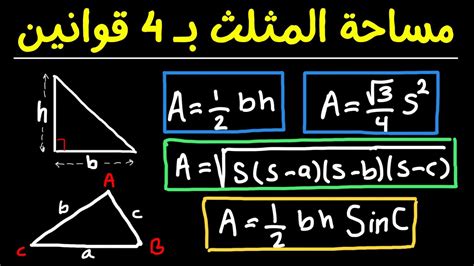
- هذه القاعدة لها قاعدة يمكن الاعتماد عليها، وهي 0.5 * طول قاعدة المثلث * ارتفاع المثلث.
- تمثل قاعدة المثلث طول أحد أضلاعه، ويمثل ارتفاع المثلث الخط المستقيم الذي يربط وسط قاعدة المثلث برأس المثلث المقابل له.
2- باستخدام صيغة هيرون
- يمكننا أيضًا الاعتماد على صيغة هيرون الهندسية لحساب مساحة المثلث بدقة، الأمر الذي يتطلب معرفة جميع أطوال الأضلاع الثلاثة للمثلث.
- أولًا، نوجد محيط المثلث بجمع أطوال الثلاثة، ثم نضربه في 0.5، ثم نستخدم صيغة هيرون حتى نتمكن من الوصول إلى مساحة المثلث من خلال الجذر التربيعي.
- هذه القاعدة لها قاعدة يجب الاعتماد عليها وهي نصف محيط نصف * نصف المحيط – الطول المحدد للضلع الأول من المثلث، وتتكرر العملية على الصلع الثاني والجانب الثالث، والنتائج الثلاثة معا.
3- باستخدام طول ضلع واحد في مثلث متساوي الأضلاع
- تعتبر طريقة استخدام طول ضلع واحد في مثلث متساوي الأضلاع من أهم الطرق والقواعد التي يتم استخدامها هندسيًا لمعرفة كيفية حساب مساحة المثلث، والتي توجد قاعدة رياضية أساسية يجب الاعتماد عليها على.
- هذه القاعدة لها قاعدة يمكن الاعتماد عليها، وهي 3/4 × 3/4 مضروبًا في مربع الضلع.
4- باستخدام علم المثلثات
- تعتبر طريقة استخدام علم المثلثات من أهم الطرق والقواعد المستخدمة هندسيًا لمعرفة كيفية حساب مساحة المثلث، والتي لها قاعدة رياضية أساسية يتم الاعتماد عليها.
- في هذه القاعدة، نحتاج إلى قياس ضلعي المثلث بجوار بعضهما البعض، وأن يكون لدينا زاوية واحدة مشتركة لدينا قياسها أيضًا.
- وهذه القاعدة لها قاعدة تعتمد عليها وهي 0.5 * حجم الضلع الأول * حجم الضلع الثاني * درجة الزاوية بين الضلعين.
ما تصريفات زوايا المثلثات
- هناك ما يعرف بالاقتران الموجود بين زوايا المثلثات، والذي يحدث بين زوايا أقل من 90 درجة، أي أن الاقتران يحدث دائمًا عند الزوايا الحادة للمثلثات المقابلة للزوايا القائمة.
- يمكننا القول إن أدوات التوصيل هي النسب بين قيم الضلعين في نفس المثلث، حيث يكون المجموع مساويًا للنسبة بين قيمة كل ضلع من أضلاع المثلث على حدة.
أنواع الاقترانات المثلثية في الهندسة وعلم المثلثات
- هناك بعض الرموز، أو ما هو معروف في لغة الرياضيات والهندسة، فالجيوب الأصلية يرمز لها باجة، وجيب التمام يرمز له بباخا، والظل يرمز له بظ، والظل يرمز له بزا، والقاطع يرمز لها باكا، وجيب التمام يرمز لها قاء.
- Ja x = حساب حجم ضلع رمز x / وتر المثلث.
- Cos x = تحسب حجم زاوية الضلع المجاورة للزاوية / حجم الوتر للمثلث.
- Z x = محسوبًا على حجم جانب الزاوية بالرمز x / احسب الضلع الموجود بجوار الزاوية x، ومن الممكن الحصول على نفس النتيجة بقسمة xx على s x.
- قياس x = حجم وتر المثلث / حساب الضلع المجاور للزاوية x.
- الوقت x = حجم وتر المثلث / احسب الضلع المقابل بجانب الزاوية x.
- X x = احسب الضلع المجاور للزاوية x / احسب الضلع المقابل للزاوية x، ومن الممكن الحصول على نفس النتيجة بقسمة xx على xx وأيضًا بقسمة الوقت x على x أيضًا.
تعلمنا معكم في هذا المقال كيفية حساب مساحة المثلث بمختلف أنواعه، وقد أوضحنا القوانين الرياضية لذلك، من خلال شرح القواعد والقوانين التي توضح كيفية استخدامه هندسيًا.